Come molti commentatori del settore hanno notato, il secondo sedile della Red Bull negli ultimi anni non è stato esattamente un sedile comodo per chiunque ci si sia seduto, per cui non è detto che questa promozione sia una buona cosa per Hadjar, che in ogni caso ha già messo come si suol dire le "mani avanti", affermando qualcosa del tipo "è impossibile battere Max". In questo senso le premesse rispetto ai suoi predecessori sono sicuramente migliori, visto che la sua idea sembra essere quella di tenere le aspettative basse (anche le sue!). Altro elemento che gioca a suo favore è che la Red Bull è cambiata abbastanza da aver creato un ambiente che potrebbe essere molto più paziente rispetto a come lo è stato con i precedenti piloti che hanno affiancato Verstappen.
Non è, però, su questi discorsi che voglio concentrami, ma, come intuibile dal titolo, sul casco che Hadjar ha portato in giro per il mondo nel corso di questo 2025. E se non ne ho scritto prima, è per il semplice motivo che solo a fine stagione ho scoperto, leggendo questo articolo, che il padre di Isack, Yassine Hasjar, è un fisico.
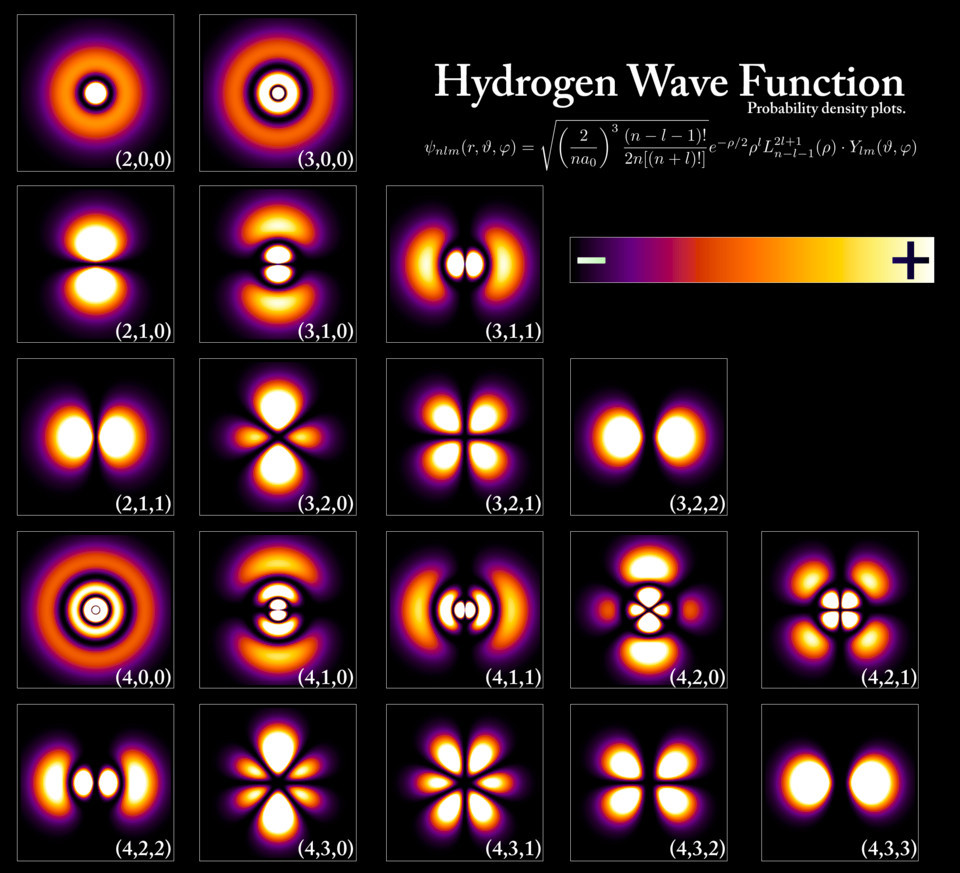
Questi, come si può dedurre dal suo profilo su Reasearch Gate, è ricercatore presso l'Università della Tecnologia di Troyes (Université de Technologie de Troyes), in Francia, dove si occupa di nanofisica e ottica quantistica. E ha, evidentemente, disegnato il casco del figlio, che è diventato una celebrazione vera e propria della fisica e di molti dei suoi protagonisti, come Albert Einstein, Max Palck, Erwin Schrodinger (il cui nome sul casco è scritto male...), Werner Heisenberg e altri.